第五周作业
1. $O(n\log{n})$的LIS算法
S:令$tail[i]$表示长度为$i$的LIS的结尾的最小值
R:枚举$A[j]$,二分查找第一个满足$A[j] > tail[i-1]$的位置,$tail[i]=A[j]$,找不到就把$A[j]$push_back进去
T:$j$增加
B:$tail$为空
O:$tail$的长度
T:$O(n) \cdot O(\log{n})_\text{(二分查找)}=O(n\log{n})$
2. Range Partial Sum Query中需要使用到寻找区间$[l,r]$跨过的中线,给出一个$O(1)$找到这个中线的方法
$mid=l+(r-l) / 2$
3. $\pm 1$RMQ的块内块间如何$O(n)$预处理,以及如何$O(1)$回答
块间:使用ST表进行预处理,时间复杂度$O(\frac{N}{L}\log{\frac{N}{L}})<O(\frac{2N}{\log{N}}\log{N})=O(N)$
块内:使用ST表进行预处理,时间复杂度$O(2^L\cdot L\log{L})=O(\sqrt{N}\log{N}\log{\log{N}})$;或暴力预处理$O(2^L\cdot L^3)=O(\sqrt{N}\left(\log^{N}\right)^3)$,当大约$N>10^6$时小于$O(N)$
回答询问:例如求$[l,r]$间的最小值,$a,b$是$l$后面最近的块起点和$r$前面最近的块终点,那就是$\min\left\{ RMQ_{块内}[l, a),RMQ_{块间}[a, b], RMQ_{块内}(a, r]) \right\}$,由于预处理过了所以回答是$O(1)$的。
4. 画出课上提到Bowling问题状态转移对应的DAG
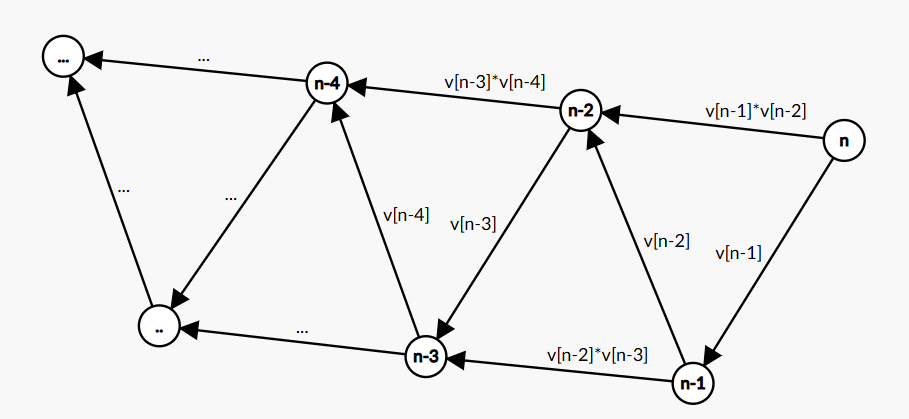
5. $O(n)$求树的直径,边权可能为负
S:令$dis[u]$表示从$u$点向它的子树出发能到达的最长距离
R:先更新$maxd = \max{\{maxd, dis[u] + dis[v] + E(u, v).w\}}$(从节点$u$出发的两条不同路径)
再更新$dis[u]=\max{\{dis[u], dis[v] + E(u, v).w\}}$
T:DFS遍历
B:$dis[]=0$
O:$maxd$
T:$O(n)$
6. $O(n^3)$解决环形石子合并问题
$N$个环形石子合并可以拆成$2N$个横排石子合并。
S:令$v[len][i][j]$代表区间长度$len$、从$i$合并到$j$的代价
R:$v[i][i+len-1] = \min\limits_{i\leq k\leq i+len-1}{\left\{ v[i][k] + v[k+1][i+len-1]+\sum\limits_{x=i}^{j}{a[x]} \right\}}$(可用前缀和优化)
T:$len:2\rightarrow n, i:1\rightarrow 2n-len+1, $
B:$v[i][i]=a[i]$,其余为$+\infty$
O:$v[1][n]$
T:$O(n^3)$
