算法设计与分析 作业3

第三周作业

1. 定义witness为运行Bellman-Ford算法n轮时距离依然减少的点。

(a) 证明：每一个负环上至少存在一个witness

设某个负环上有$l_i(l_i\leq n)$个点，显然，至多$l_i$轮就可以将这个负环上的距离更新一遍。

当$l_i=n$时，这个负环上的witness就是最后一个更新的点；当$l_i<n$时，在剩余的轮里，一定可以从这个点出发，更新负环内的其它点，因此环上一定存在一个witness。

(b) 构造一张图使得至少存在一个witness不在负环上

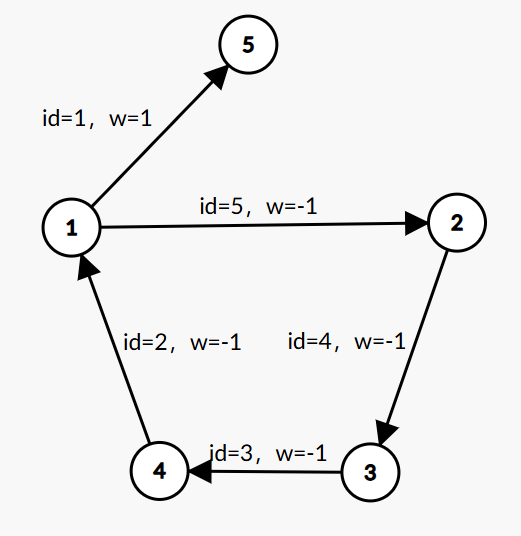
以点1为源点计算最短路，按边1、2、3、4、5的顺序更新。

第一轮：$d_1=0, d_2=-1,d_3=d_4=\infty,d_5=1$

第四轮：$d_1=-4, d_2=-1,d_3=-2，d_4=-3,d_5=1$

第五轮：$d_1=-4, d_2=-5,d_3=-2，d_4=-3,d_5=-3$，witeness为点2和点5，其中点5不在负环上。

2. DAG中的单源最短路可以在$O(|V|+|E|)$的时间内求解。求解步骤为：1、求出图的拓扑序；2、根据拓扑序对每个节点进行松弛。

(a) 写出算法的伪代码

def SSSP_DAG(G, s):
    dis = [infty for _ in G.V]
    dis[s] = 0
    
    topo = topo_sort(G)
    for u in topo:
        for e in G.E[u]:
            if dis[u] + e.w < dis[e.to]:
                dis[e.to] = dis[u] + e.w
    return dis

(b) 说明为什么按照拓扑序的松弛得到的结果是正确的

对于拓扑序排在s点前的点，根据DAG的性质，s点无法到达这些点，因此这些点的dis为正无穷是正确的。

对于拓扑序排在s点后的点，根据拓扑排序的性质，一定是拓扑序在前面的点处理完毕后才可以处理后边的点。这样就可以保证，前驱节点在松弛当前节点的时候就已经正确计算完毕了，所以结果是正确的。

3. Dijkstra算法只适用于求边权非负的图的最短路，如果存在负权边则算法的正确性不能保证。但是，假如运行Dijkstra多次呢？假设一张图中有$k-1$条负权边，但不存在负环，运行$k$次Dijkstra算法，每次运行结束后，从源点向每个节点连一条长度为$d(s,u)$的边，证明这样正确的求出源点到每个点的距离。

Dijkstra不能处理负边的原因，在于不能对已确定最短路径的点进行二次更新（vis这个数组）。

将上一轮的最短路结果连边，进行新的一轮，相当于在已确定最短路径的点进行二次更新，这样就可以保证正确求出最短路。

运行$k$次可以保证因$k-1$条负权边引起的二次修改都能被满足。

4. 无向图中x到y的最小瓶颈路是这样的一类简单路径，满足这条路径上的最大的边权在所有x到y的简单路径中最小。

(a) 证明：任意一棵最小生成树上x到y的路径就是原图中x到y的最小瓶颈路

反证：假设存在一条$x$到$y$的最小瓶颈路，路径$R’$上最大边权$w(e’)$比最小生成树上的路径$w(e)$还小。那么我们可以删去树上$e’$这条边，用最小瓶颈路上的边连接这两个连通块，新树的边权之和一定比原来还小，与最小生成树矛盾。

(b) 最小生成树上x到y的路径一定是原图中x到y的最小瓶颈路，但是并不是x到y的所有最小瓶颈路都在某棵最小生成树上，构造一张图使得x到y的一条最小瓶颈路不在任何一棵最小生成树上。

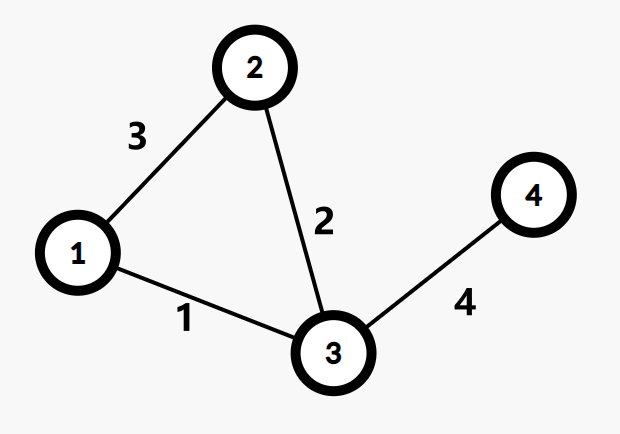
路径1-2-3-4和1-3-4都是最小瓶颈路，但1-2这条边一定不会出现在最小生成树上。

5.

(a) 说明对于一般的图，如何用Bellman-Ford算法使用的$O(nm)$时间判断图中是否存在负环。（不一定所有点都从源点可达）

用并查集维护连通块，对每一个连通块运行Bellman-Ford算法进行判断。

(b) 假设一张图不存在负环，说明如何用Bellman-Ford算法判断一张图是否存在零环

由于没有负环，那么零环一定满足：环上一点到它环中前驱的的最短路（否则就出现负环了），等于前驱到它边权的相反数。

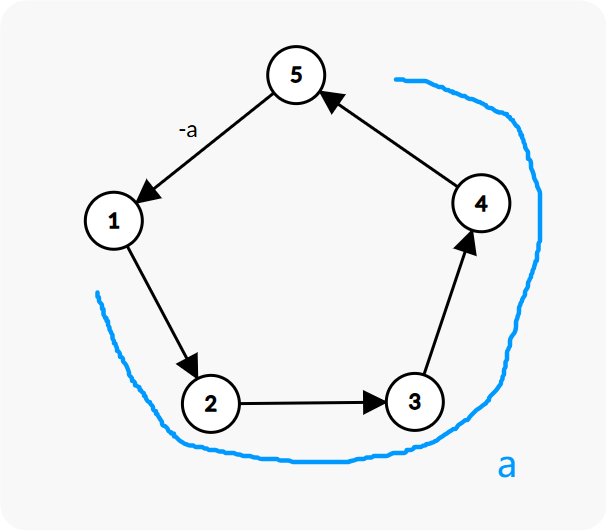
那么就可以对所有点跑一遍Bellman-Ford最短路，枚举所有有边指向起点且一步相连的点，看最短路和边权相加是否为0即可。

时间复杂度$O(n^2m)$

(c) 求最小权重比率环

EPS = 1e-7

def relax(dis, (u, v, w), alpha):
    if dis[u] + w - alpha < dis[v]:
        dis[v] = dis[u] + w - alpha
        return True
    return False
        
def BellmanFord(G, s, mid):
    dis = [infty for n in G.N]
    dis[s] = 0
    for n in G.N:
        flag = False
        for e in G.V:
            flag |= relax(e, mid)
    return flag

def erfen(s):
    l = -M
    r = M
    mid = (l + r) / 2
    while True:
        if BellmanFord(G, s, mid) == True: # 存在负环
            r = mid
        else:
            l = mid
        mid_new = (l + r) / 2
        if math.abs(mid_new - mid) < EPS:
            break
        mid = mid_new
    return mid

---

Solution