算法设计与分析 作业7

第七周作业

1. 二分图匹配

利用匈牙利算法进行二分图最大匹配。若匹配数和点数$N$相等，则回答Y，否则回答N。

匈牙利算法

令$p_v$表示与$V$中点$v$配对的$U$中的点，$t_v$表示是否尝试过与$u$配对的点。

对于$U$中的每个元素$u$，枚举$V$中所有与$u$有连边、且未尝试过与$u$配对的点$v$：如果$v$未与其它$U$中的点匹配，则$u$与$v$匹配；否则枚举所有$V$中与$p_v$有连边、且未尝试过与$u$配对的点$v’$：如果$v’$未与其它$U$中的点匹配，则$p_v$与$v’$匹配、$u$再与$v$匹配；否则枚举所有$V$中与$p_{v’}$有连边的点$v’’$：……

def Find(u):
    for v in u.E:
        if not t[v]:
            t[v] = True
            if !p[v] or Find(p[v]):
                p[v] = u
                return True
    return False
def Hungarian():
    count = 0
    t = [None for _ in range(N)]
    for u in U:
        t = [False for _ in range(N)]
        if Find(u):
            count += 1
    return count == N, p

时间复杂度$O(N)\text{\small(枚举$U$中所有点)}\cdot O(|E|)\text{\small(枚举所有边)}=O(N|E|)$

也可以将源点连上左边所有点，右边所有点连上汇点，容量均为$1$。原来的每条边从左往右连边，容量也均为$1$，最大流即最大匹配。用Dinic网络最大流，可在$O(\sqrt{N}|E|)$内求出。

2. Rod Cutting问题的Relation改为$x(l)=\max{\left\{ x(p)+x(l-p),v(l) | p\in\left\{ 1, \dots, l \right\} \right\}}$后的时间复杂度

$l$升序枚举，从$1$到$L$；取$\max$时需要$p$从$1$到$l$枚举，比$l$小的$x(p)$和$x(l-p)$已经计算过了，可以$O(1)$得到。

所以时间复杂度为$O(L^2)$

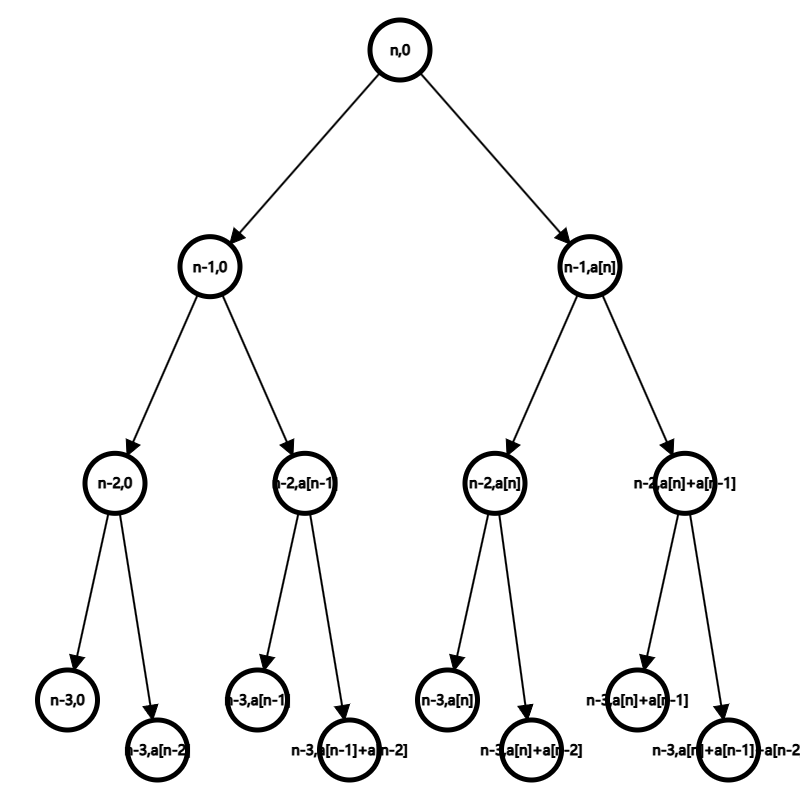
3. 画出Subset Sum问题的计算有向无环图

$$\cdots \cdots$$

4. 画出一个无法被满足的3SAT问题$\Phi$对应的3DM的实例

$$\Phi=\left( x_1 \lor \neg x_2 \lor x_3 \right) \land \left( \neg x_1 \lor x_2 \lor x_3 \right) \land \left( x_1 \lor x_2 \lor \neg x_3 \right) \land \left( \neg x_1 \lor \neg x_2 \lor \neg x_3 \right) \land \left( \neg x_1 \lor \neg x_2 \lor x_3 \right) \land \left( x_1 \lor \neg x_2 \lor \neg x_3 \right)$$

Solution