清北澡堂2020十一刷题Day1 解题报告
[思路题]T1 打扑克
我是sb
一道sb题 推了2+hours 啥也不会
分情况讨论,大概就是$
\begin{cases}
n为偶数\begin{cases}奇数先出\\偶数先出\end{cases}\\
n为奇数\begin{cases}奇数先出\\偶数先出\end{cases}\\
\end{cases}
$
首先,我们可以把奇数组中的$n$和偶数组中的$n+1$划到一个组中
默认「你」是先出的那一方
$n$为奇数
以$\begin{align}1\qquad2\\3\qquad4\\5\qquad\ \ \\\end{align}$为例
奇数先出
可以发现,如果从最小的数$1$开始从小到大出,最后会剩下$5$出不去($1-2,\ 3-4,\ \cdots$)
所以要创造一次偶数方无法出牌的情况,来使多余的那张牌出去
只要先将最大点数的牌出掉,然后再出剩下的牌,对手出$n$,你就出$n+1$,即为必胜策略
即$ans_{n \& 1 == 1 \&\&op\&1==0}=0$
偶数先出
只要你先出,对手总会有一张牌出不掉
所以$ans_{n \& 1 == 1 \&\&op\&1==1}=1$
所以,$ans_{n\&1==1}=op$
$n$为偶数
以$\begin{align}1\qquad2\\3\qquad4\\5\qquad6\\\end{align}$为例
n == 2
先手必胜
奇数先出
对手的必胜策略是,不管你第一步出的什么,对手都出最大的一张牌
这样不管你怎样出,也会剩下一张牌出不出去
所以$ans_{n \& 1 == 0 \&\& op\&1==1} = 1$
偶数先出
按上面的必胜策略出即可
所以,$ans_{n \& 1 == 0}=\begin{cases}op&n==2\\1&n\neq2\end{cases}$
综上,$ans=\begin{cases}op&n==2或n为奇数\\1&n为偶数且n\neq2\end{cases}$
[思路题]T2 粉刷匠
emm 妙啊
Subtask 1: 30pts
暴力模拟即可
Subtask 2: 60pts
听说开10棵线段树,维护即可
100pts
首先,最后的答案只与最后粉刷的颜色有关,所以可以倒序处理染色操作
如图,最后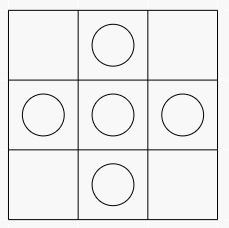 的粉刷结果可以转化为
的粉刷结果可以转化为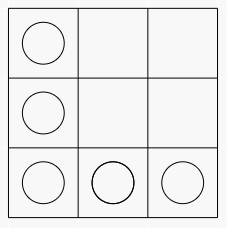 这样的结果(圈为染成蓝色的点)
这样的结果(圈为染成蓝色的点)
所以,可以一边刷墙一边统计答案,因为染色过的格子,再次染色不会受到影响
所以染过某一行或者某一列之后,可以直接--行数或者--列数,在这之前,要统计答案
Code
1 | for (register int i = k; i > 0; --i) |
[暴力辗标算]T3 直线竞速
暴力碾标算?
没开
long long见祖宗
100pts #1
就是每次计算所有人当前时间的位置pos
用sort或者nth_element对pos排序求即可
100pts #2
显然,每两个选手之间,交换排名的次数至多有一次
所以总交换次数为$\dfrac{n\cdot(n-1)}{2}$
所以可以按时间把每次询问排序,
每次询问冒泡排序选手位置即可
课件中说:
总的交换次数是$O(n^2)$的
时间复杂度$O(n^2+nQ+QlogQ)$
Code
1 | for (register int i = 0; i <= q; ++i) { |
